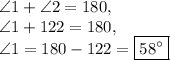Question

PLEASE ANSWER!! I don’t understand

Answer 1

`m\angle 2=122^(\circ),\\m\angle 1 = 58^(\circ)`

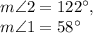
Explanation:

By definition, tangent lines touch a circle at one point. This one point intersects the circle at a 90 degree angle.

In any circle, the measure of an inscribed angle is exactly half of the arc it forms. Since
`\angle 2` forms an arc labelled 244 degrees, the measure of angle 2 must be
`(244)/(2)=\boxed{122^(\circ)}`.

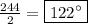Angle 1 and 2 form one side of a line. Since there are 180 degrees on each side of the line, we have:

`\angle 1+\angle 2=180,\\\angle 1 + 122=180,\\\angle 1=180-122=\boxed{58^(\circ)}`