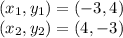Answer:
Explanation:
we are given two conditions
- two integers whos product is -12
- two integers whos sum is 1
let the two integers be x and y respectively according to the first condition
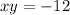
according to the second condition:
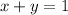
now notice that we have two variables therefore ended up with a simultaneous equation so to solve the simultaneous equation cancel x from both sides of the second equation which yields:
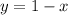
now substitute the got value of y to the first equation which yields:
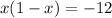
distribute:
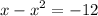
add 12 in both sides:
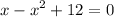
rearrange it to standard form:
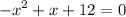
divide both sides by -1:

factor:
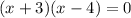
by Zero product property we acquire:
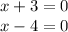
solve the equations for x therefore,
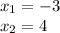
when x is -3 then y is
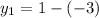
simplify
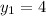
when x is 4 y is
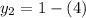
simplify:
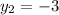
hence,