Question

About 9% of the population has a particular genetic mutation. 900 people are randomly selected. Find the standard deviation for the number of people with the genetic mutation in such groups of 900.

Answer 1

The standard deviation is of 8.586.

Explanation:

For each person, there are only two possible outcomes. Either they have a genetic mutation, or they do not. The probability of a person having the mutation is independent of any other person, which means that the binomial probability distribution is used to solve this question.

Binomial probability distribution

Probability of exactly x successes on n repeated trials, with p probability.

The standard deviation of the binomial distribution is:

`√(V(X)) = √(np(1-p))`

About 9% of the population has a particular genetic mutation.

This means that
`p = 0.09`

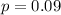
900 people are randomly selected.

This means that
`n = 900`

Find the standard deviation for the number of people with the genetic mutation in such groups of 900.

`√(V(X)) = √(900*0.09*0.91) = 8.586`

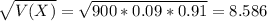
The standard deviation is of 8.586.