Answer:
None of the options is true
Explanation:
Given

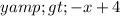
Required
Which makes the above inequality true
The missing options are:
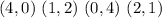
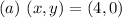
Substitute values for x and y in the inequalities


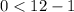
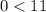 ---- This is true
---- This is true
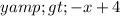

 --- This is false
--- This is false
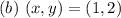
Substitute values for x and y in the inequalities


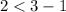
 --- This is false (no need to check the second inequality)
--- This is false (no need to check the second inequality)
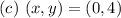
Substitute values for x and y in the inequalities



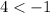 --- This is false (no need to check the second inequality)
--- This is false (no need to check the second inequality)
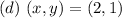
Substitute values for x and y in the inequalities


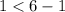
 --- This is true
--- This is true
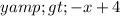
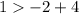
 -- This is false
-- This is false
Hence, none of the options is true