Answer:
The number of ways is 26,400 ways
Explanation:
Given;
total number of men, M = 10
total number of women, W = 12
number of committees to be formed = 6
If there must be equal gender, then it must consist of 3 men and 3 women.
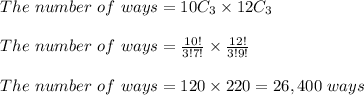
Therefore, the number of ways is 26,400 ways