Question

The following integral requires a preliminary step such as long division or a change of variables before using the method of partial fractions. Evaluate the following integral. x^4 + 7/x^3 + 2x dx Find the partial fraction decomposition of the integrand. x^4 + 7/x^3 + 2x dx

Answer 1

Division yields

`(x^4+7)/(x^3+2x) = x-(2x^2-7)/(x^3+2x)`

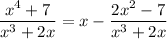
Now for partial fractions: you're looking for constants a, b, and c such that

`(2x^2-7)/(x(x^2+2)) = \frac ax + (bx+c)/(x^2+2)`

`\implies 2x^2 - 7 = a(x^2+2) + (bx+c)x = (a+b)x^2+cx + 2a`

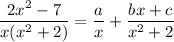
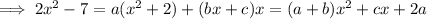
which gives a + b = 2, c = 0, and 2a = -7, so that a = -7/2 and b = 11/2. Then

`(2x^2-7)/(x(x^2+2)) = -\frac7{2x} + (11x)/(2(x^2+2))`

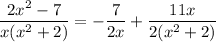
Now, in the integral we get

`\displaystyle\int(x^4+7)/(x^3+2x)\,\mathrm dx = \int\left(x+\frac7{2x} - (11x)/(2(x^2+2))\right)\,\mathrm dx`

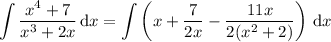
The first two terms are trivial to integrate. For the third, substitute y = x ² + 2 and dy = 2x dx to get

`\displaystyle \int x\,\mathrm dx + \frac72\int\frac{\mathrm dx}x - \frac{11}4 \int\frac{\mathrm dy}y \\\\ =\displaystyle \frac{x^2}2+\frac72\ln|x|-\frac{11}4\ln|y| + C \\\\ =\displaystyle \boxed{\frac{x^2}2 + \frac72\ln|x| - \frac{11}4 \ln(x^2+2) + C}`