1 Answer

Arko Elsenaar · Answer 1 · 2022-12-06T13:02:32+0000

Answer:

The function that passes through (0, 0) is
$f(x) = (1)/(6)\cdot e^{2\cdot x^(3)} - (1)/(6)$ .

Explanation:

Firstly, we integrate the function by algebraic substitution:

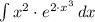$\int {x^(2)\cdot e^{2\cdot x^(3)}} \, dx$ (1)

If
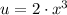$u = 2\cdot x^(3)$ and
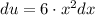$du = 6\cdot x^(2) dx$ , then:

$\int {e^{2\cdot x^(3)}\cdot x^(2)} \, dx$

$(1)/(6)\int {e^(u)} \, du$

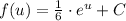
$f(u) = (1)/(6)\cdot e^(u) + C$

$f(x) = (1)/(6)\cdot e^{2\cdot x^(3)} + C$

Where
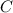is the integration constant.

If
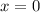x = 0 and
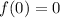f(0) = 0 , then the integration constant is:

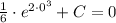
$(1)/(6)\cdot e^{2\cdot 0^(3)} + C= 0$

C = -(1)/(6)

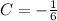
Hence, the function that passes through (0, 0) is
$f(x) = (1)/(6)\cdot e^{2\cdot x^(3)} - (1)/(6)$ .

Please log in or register to add a comment.