Note: There must be -4 instead of 4 otherwise all options are incorrect.
Given:
A polynomial function has a leading coefficient of 3 and roots -4, 1, and 2, all with multiplicity 1.
To find:
The polynomial function.
Solution:
The general polynomial function is defined as:

Where, a is the leading coefficient,
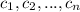 are the zeros with multiplicity
are the zeros with multiplicity
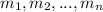 respectively.
respectively.
It is given that a polynomial function has a leading coefficient of 3 and roots 4, 1, and 2, all with multiplicity 1. So, the polynomial function is defined as:
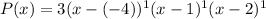
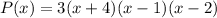
Therefore, the correct option is A.