Question

Match the following items by evaluating the expression for x = -2.

Answer 1

1)¼

2)½

3)1

4)2

5)4

Explanation:

Question-1&2:

recall that,

`\displaystyle {x}^( - n) = \frac{1}{ {x}^(n) }`

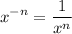
we want to evaluate
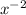`x^(-2)` for x=-2

to do so substitute the given value of x

`\displaystyle {2}^( - 2)`

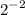
apply the formula:

`\displaystyle {2}^( - 2) = \frac{1}{ {2}^(2) }`

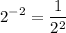
simplify square:

`\displaystyle {2}^( - 2) = \boxed{(1)/( 4) }`

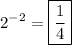
likewise substitute the given value of x to x^-1:

`\displaystyle {2}^( - 1)`

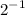
apply the formula:

`\displaystyle {2}^( 1) = \frac{1}{ {2}^(1) }`

`\displaystyle {2}^( 1) = \boxed{\frac{1}{ {2}^{} } }`

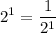
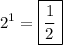
Question-3:

substitute the value of x

`\displaystyle {2}^( 0)`

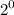
it's a universal truth that x⁰=1 Thus

`\displaystyle \boxed{1}`

Question-4&5:

Substitute the given value of x to x¹ and x² respectively

`\displaystyle {2}^( 1) \quad \bigg | \quad {2}^(2)`

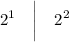
simplify:

`\displaystyle \boxed{2} \quad \bigg | \quad \boxed4`

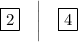
and we're done!

Answer 2

see below

Explanation:

x^-2 = 1/x^2 Let x = -2 1/ (-2)^2 = 1/4

x^-1 = 1/x^1 Let x = -2 1/ (-2)^1 = 1/(-2) = -1/2

x^0 = 1

x^1 = x Let x = -2 (-2)

x^2 = Let x = -2 (-2)^2 = 4