The cylindrical water tank on a semitrailer has a length of 20 feet. The volume of the tank is equal to the product of pi, the square radius of the tank, and the length of the tank.
Let V represent the volume of the tank, r represent the radius of the tank, and h represent the length of the tank.
Part A.
Create an equation that could be used to find the volume, V, of the cylindrical tank.
Part B.
Rewrite the volume formula to create an equation that can be used to calculate the radius, R, of the water tank.
Drag the terms to the correct locations in the equation. Not all terms will be used.
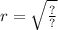
20h, 20pi, 20V, V, 400(pi)h, i
Part C.
Graph the radical equation that can be used to calculate the radius, r, of the tank. Use lowercase "r" and the uppercase "V" when typing the equation.
Part D.
Suppose the cylindrical water tank has a radius of 12 feet. Use this information and the equation modeling the radius of the tank to complete these statements.
The volume of the water tank is about [4,000], [9,048], [754], or [2,880] cubic feet.