Answer:
The p-value of the test is 0.0066 < 0.05, which means that there is sufficient evidence at the 0.05 significance level to conclude that the mean salary differs from $39,385
Explanation:
The average salary for public school teachers for a specific year was reported to be $39,385. Test if the mean salary differs from $39,385
At the null hypothesis, we test if the mean is of $39,385, that is:
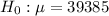
At the alternative hypothesis, we test if the mean differs from this, that is:
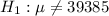
The test statistic is:
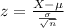
In which X is the sample mean,
 is the value tested at the null hypothesis,
is the value tested at the null hypothesis,
 is the standard deviation and n is the size of the sample.
is the standard deviation and n is the size of the sample.
39385 is tested at the null hypothesis:
This means that
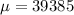
A random sample of 50 public school teachers in a particular state had a mean of $41,680, and the population standard deviation is $5975.
This means that
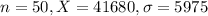
Value of the test statistic:
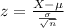
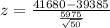
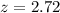
P-value of the test and decision:
The p-value of the test is the probability that the sample mean differs from 39385 by at least 2295, which is P(|Z| > 2.72), which is 2 multiplied by the p-value of Z = -2.72.
Looking at the z-table, Z = -2.72 has a p-value of 0.0033
2*0.0033 = 0.0066
The p-value of the test is 0.0066 < 0.05, which means that there is sufficient evidence at the 0.05 significance level to conclude that the mean salary differs from $39,385