Answer:
The farmer should plant 14 additional trees, for maximum yield.
Explanation:
Given
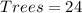
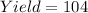
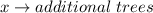
So, we have:
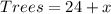
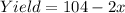
Required
The additional trees to be planted for maximum yield
The function is:
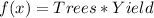

Open bracket

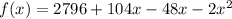
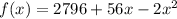
Rewrite as:

Differentiate

Equate
 to 0 and solve for x to get the maximum of x
to 0 and solve for x to get the maximum of x

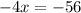
Divide by -4

The farmer should plant 14 additional trees, for maximum yield.