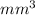The question is incomplete. The complete question is :
Cylinders A and B are similar. The length of the cylinder A is 4 mm and the length of cylinder B is 6 mm. The volume of cylinder A is 20mm3. Calculate the volume of cylinder B.
Answer:
67.5
Explanation:
Given that :
Cylinder A and cylinder B are similar.
Let volume of cylinder A = 20
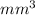
We know the volume of a cylinder is given by V =
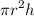
where, r is the radius of the cylinder
h is the height of the cylinder
We have to find the scale factor.
The length scale factor is =

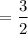
Area scale factor
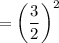
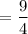
∴ Volume scale factor
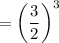
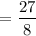
Therefore, the volume of cylinder B is
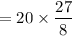
= 67.5