Question

Show A and Show B are two of the most popular television shows of all time. The number of episodes of each show are consecutive even integers whose sum is 570. If there are more episodes of Show A, how many episodes of each were there?

Answer 1

A = 286 episodes

B = 284 episodes

Explanation:

Let n = the
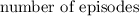`\text{number of episodes}` of show B

n + 2 = the
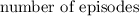`\text{number of episodes}` of show A

Therefore, according to the question,

The sum of the number of the episodes of each show are consecutive even integers = 570

Therefore,

n + n + 2 = 570

2n + 2 = 570

2n = 568

n = 284

Therefore, the number of episodes for B = 284

The number of episodes for A = n + 2 = 284 + 2

= 286