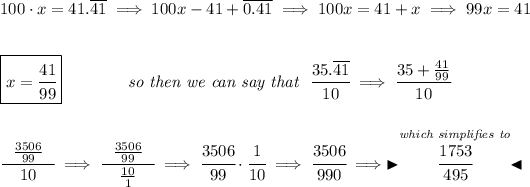Question

I need someone to please explain how to turn this into a simplified fraction. (NOTE: please explain!!) __ 3.541 The repeating sign is only above the 41, not the five

Answer 1

the way to do these recurring decimals is by firstly separating the repeating part or recurring part and then multiply it by some power of 10 so we move it to the left, lemme show

`3.5\overline{41}\implies \cfrac{35.\overline{41}}{10}\qquad \stackrel{\textit{say that the repe}\textit{ating part is }~\hfill }{x = \overline{0.41}\qquad \qquad \textit{so that }35.\overline{41}=35+\overline{0.41}=35+x}`

now, let's multiply that repeating part by some power of 10 that moves the 41 to the left, well, we have two repeating decimals, 4 and 1, so let's use two zeros, namely 100 or 10², thus

`100\cdot x = 41.\overline{41}\implies 100x - 41+\overline{0.41}\implies 100x = 41+x\implies 99x=41 \\\\\\ \boxed{x =\cfrac{41}{99}}\qquad \qquad \textit{so then we can say that}~~\cfrac{35.\overline{41}}{10}\implies \cfrac{35+(41)/(99)}{10} \\\\\\ \cfrac{~~(3506)/(99)~~}{10}\implies \cfrac{~~(3506)/(99)~~}{(10)/(1)}\implies \cfrac{3506}{99}\cdot \cfrac{1}{10}\implies \cfrac{3506}{990}\implies \blacktriangleright \stackrel{\textit{which simplifies to}}{\cfrac{1753}{495}} \blacktriangleleft`