Question

A field is 360 feet long and 160 feet wide. Sod can be purchased in squares in increments from 1 foot wide up to 7 feet wide. What is the largest size squares Steve can purchase with which he can cover the field completely without any gaps or overhangs?

Answer 1

We need 1600 squares with a width of 6 feet to cover the entire field without any gaps nor overhangs.

Explanation:

The number of squares required to cover the field is equal to the area of the field divided by the area of a square:

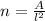`n = (A)/(l^(2))` (1)

Where:

`n` - Quantity of squares, in feet.

`A` - Area of the field, in square feet.

`l` - Length of each square, in feet.

If we know that
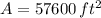`A = 57600\,ft^(2)`, then we have the following hyperbolic function:

`n = (57600)/(l^(2))`

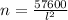
Now we plot the function with the help of graphing tools, whose result is presented below. Please notice that quantity of squares must be an integer and we need 1600 squares with a width of 6 feet to cover the entire field without any gaps nor overhangs.