Answer:
A) v_{f1} = -3.2 m / s, B) LEFT , C) v_{f2} = -0.12 m / s, D) LEFT
Step-by-step explanation:
This is a collision exercise that can be solved using momentum conservation, for this we define a system formed by gliders, so that the forces during the collision are internal and the moment is conserved.
Let's use the subscript 1 for the lightest glider m1 = 0.160 kg and vo1 = 0.820 m / s
subscript 2 for the heaviest glider me² = 0.820 kg and vo2 = -2.27 m / s
Initial instant. Before the crash
p₀ = m₁ v₀₁ + m₂ v₀₂
Final moment. After the crash
p_f = m₁ v_{f1} + m₂ v_{f2}
p₀ = p_f
m₁ v₀₁ + m₂ v₀₂ = m₁ v_{f1} + m₂ v_{f2}
as the shock is elastic, energy is conserved
K₀ = K_f
½ m₁ v₀₁² + ½ m₂ v₀₂² = ½ m₁
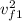 + ½ m₂
+ ½ m₂
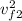
m₁ (v₀₁² - v_{f1}²) = m₂ (v_{f2}² -v₀₂²)
let's make the relationship
(a + b) (a-b) = a² -b²
m₁ (v₀₁ + v_{f1}) (v₀₁-v+{f1}) = m₂ (v_{f2} + v₀₂) (v_{f2} -v₀₂)
let's write our two equations
m₁ (v₀₁ -v_{f1}) = m₂ (v_(f2) - v₀₂) (1)
m₁ (v₀₁ + v_{f1}) (v₀₁-v_{f1}) = m₂ (v_{f2} + v₀₂) (v_{f2} -v₀₂)
we solve
v₀₁ + v_{f2} = v_{f2} + v₀₂
we substitute in equation 1 and obtain
M = m₁ + m₂
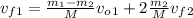
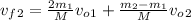 vf2 = 2m1 / mm vo1 + m2-m1 / mm vo2
vf2 = 2m1 / mm vo1 + m2-m1 / mm vo2
we calculate the values
m₁ + m₂ = 0.160 +0.3000 = 0.46 kg
v_{f1} =
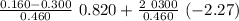
v_{f1} = -0,250 - 2,961
v_{f1} = - 3,211 m / s
v_{f2} =
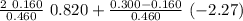
v_{f2} = 0.570 - 0.6909
v_{f2} = -0.12 m / s
now we can answer the different questions
A) v_{f1} = -3.2 m / s
B) the negative sign indicates that it moves to the left
C) v_{f2} = -0.12 m / s
D) the negative sign indicates that it moves to the LEFT