Question

Design and Analyze an algorithm for the following problem,

Give pseudocode for your algorithm.
Prove that your algorithm is correct.
Give the recurrence relation for the running time for your algorithm.
Solve the recurrence relation.
Suppose you are given 3n marbles that look identical, with one special marble that weighs more than the other marbles. You are also given a balancing scale that takes two items (or sets of items) and compares their weights. Design and analyze a divide and conquer algorithm to find the heavy marble using the balancing scale at most n times.

Answer 1

If you have 3n marbles, then you need at least n weighings to find the heavier marble.

Algorithm:-

Label all marbles from 1 to n.

Divide the marbles into three groups G1, G2, and G3 such 2 groups G1, and G2 are compared to every other employing a pan, and therefore the third group G3 is kept aside.

Condition 1- If G1>G2, If the special marble is one among the primary two groups that are being weighed,i.e., special marble is in G1.

Condition 2- If G2>G1, If the special marble in group 2, G2.

Condition 3- If G1=G2 If the primary two groups weigh equal, then special marble is present within the third group, G3.

Take the group containing special marble and perform the above steps 1,2,3,4 on it.

Keep repeating the above steps until, a gaggle of three marbles is obtained, and therefore the special marble is found from that group by performing steps 1,2,3,4 on the group.

Step-by-step explanation:

Pseudocode:-

function puzzle( G1, G2, G3)

{

Compare the values G1, G2

if G1>G2

return G1

else if G2>G1

return G2

else

return G3

end of function puzzle

}

function main()

{

print prompt "Enter the value of n"

Take the value of n from the user

while(n != 0)

{

Create 3 groups/arrays each of size 3n-1

G= puzzle( g1,g2,g3)

n= 3n-1

}

print the value in G

end of main

}

Recurrence relation for the running time for the algorithm:-

T (n) = 2T ( n1/3) + 1 with base T (3) = 1.,

here n is the total number of marbles.

We cannot apply the master theorem because of the cube root, so we draw the recursion tree.

First, we determine the height of the tree; denote this by h. By observing the powers of the arguments in the tree, we can see that in order to get to the base case of n = 3, it must be that,

n(1/2)h=3

(1/3)h=logn(3) = log 3/ log n = 1/log n

3h=log n

Now, since we do a constant amount of work (1, specifically) at each node in the recursion tree, we note that at depth d in the recursion tree we do 3d total work. We can therefore write the sum over the tree as a geometric series as follows:

`T(n)= \sum_(d=0)^(log(logn))3^d = (1-3^(log(log(n)+1)))/1-3)=(3^(log(log(n)+1))-1)/2\\T (n) = 3 log (n)-1`

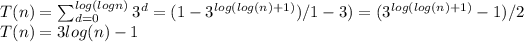
Therefore,

T (n) = Θ(log n).