Answer:
(x , y ) = ( -95, -67)
Explanation:
Given system :-
2x - 3y = 11
-6x + 8y = 34
Find :- Solutions of system by using Cramers rule.
Solution :-
To solve the system using Cramer's rule, list all needed determinants.
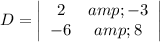
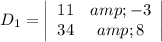

- Evaluate the determinants.
D = 8 × 2 - ( -3) ( -6 )
= 16 - 18 = -2
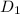 = 11 × 8 - ( -3 ) ( 34 )
= 11 × 8 - ( -3 ) ( 34 )
= 88 + 102 = 190
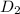 = 2 × 34 - ( 11 ) ( -6 )
= 2 × 34 - ( 11 ) ( -6 )
= 68 + 66 = 134
- Since D ≠ 0, Cramer'rs rule can be applied , so find x , y using the formulas;- x =
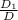 , y =
, y =
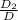 .
.
Plug the value into the formula:-
x =
 , y =
, y =
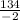 .
.
Divide
x = -95 , y = -67
- The possible solution of the system is the ordered pair ( x , y ).
(x , y ) = ( -95, -67)