Answer:
n = 2.23 moles
Step-by-step explanation:
Given the following data;
Standard temperature = 273 K
Standard pressure = 101.325 kPa
Volume = 50 liter
R = 8.314 J/mol·K
To find the number of moles, we would use the ideal gas law formula;
PV = nRT
Where;
- P is the pressure.
- V is the volume.
- n is the number of moles of substance.
- R is the ideal gas constant.
- T is the temperature.
Making n the subject of formula, we have;
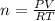
Substituting into the formula, we have;
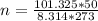
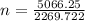
n = 2.23 moles
Therefore, 2.23 moles of carbon dioxide at STP will fit in a 50 liter container.