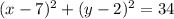Question

Find the equation of a circle with a center at (7,2) and a point on the circle at (2,5)?

Answer 1

`(x-7)^2+(y-2)^2=34`

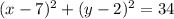
Explanation:

We want to find the equation of a circle with a center at (7, 2) and a point on the circle at (2, 5).

First, recall that the equation of a circle is given by:

`(x-h)^2+(y-k)^2=r^2`

Where (h, k) is the center and r is the radius.

Since our center is at (7, 2), h = 7 and k = 2. Substitute:

`(x-7)^2+(y-2)^2=r^2`

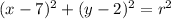
Next, the since a point on the circle is (2, 5), y = 5 when x = 2. Substitute:

`(2-7)^2+(5-2)^2=r^2`

Solve for r:

`(-5)^2+(3)^2=r^2`

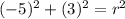
Simplify. Thus:

`25+9=r^2`

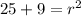
Finally, add:

`r^2=34`

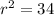
We don't need to take the square root of both sides, as we will have the square it again anyways.

Therefore, our equation is:

`(x-7)^2+(y-2)^2=34`