Question

A small planet having a radius of 1000 km exerts a gravitational force of 100 N on an object that is 500 km above its surface. If this object is moved 500 km farther from the planet, the gravitational force on it will be closest to Group of answer choices 56 N. 24 N. 77 N. 45 N. Flag question: Question 14 Question 14

Answer 1

The gravitational force will be closest to group A: 56 N.

Step-by-step explanation:

The gravitational force of the planet is given by:

`F = (GmM)/(r^(2))`

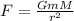
Where:

G: is the gravitational constant

m: is the mass of the object

M: is the mass of the planet

r: is the distance

When the object is 500 km above the surface of the planet, the gravitational force is 100 N:

`F_(1) = (GmM)/(r_(1)^(2)) = (GmM)/((500 km + 1000 km)^(2)) = (GmM)/((1500 km)^(2))`

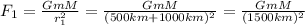
And when the object is 500 km farther from the planet, the gravitational force is given by:

`F_(2) = (GmM)/(r_(2)^(2)) = (GmM)/((500 km + 1500 km)^(2)) = (GmM)/((2000 km)^(2))`

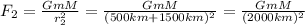
By dividing F₂ by F₁ we can calculate F₂:

`(F_(2))/(F_(1)) = ((GmM)/((2000 km)^(2)))/((GmM)/((1500 km)^(2)))`

`F_(2) = 100 N*((1500 km)^(2))/((2000 km)^(2)) = 56.2 N`

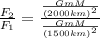
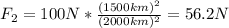
Therefore, the gravitational force will be closest to group A: 56 N.

I hope it helps you!