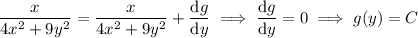Question

Evaluate the following integral over the ellipse ​

Answer 1

The underlying vector field,

F(x, y) = -y/(4x ² + 9y ²) i + x/(4x ² + 9y ²) j,

is conservative, so any integral of F over a closed path is 0.

To establish that F is conservative, we want to find a scalar function f(x, y) whose gradient is equal to F(x, y), which entails solving

`(\partial f)/(\partial x)=-\frac y{4x^2+9y^2}`

`(\partial f)/(\partial y)=\frac x{4x^2+9y^2}`

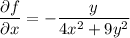
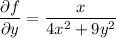
Integrating the first equation with respect to x yields

`f(x,y)=-\frac16\arctan\left((2x)/(3y)\right)+g(y)`

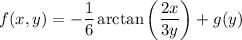
and differentiating with respect to y gives

`\frac x{4x^2+9y^2}=\frac x{4x^2+9y^2}+(\mathrm dg)/(\mathrm dy) \implies (\mathrm dg)/(\mathrm dy)=0 \implies g(y)=C`