Answer:
The z-score for a home priced at $200,000 in Florida is of -2.5.
The z-score for a home priced at $200,000 in Ohio is of 2.5.
The closeness to the mean is measured by the absolute z-score(disconsidering the signal, the lower the score, the closer to the mean). However, in this case, both z-scores have the same absolute value, so in both Florida and Ohio a home priced at $200,000 is equally close to the mean.
Explanation:
Z-score:
In a set with mean
 and standard deviation
and standard deviation
 , the z-score of a measure X is given by:
, the z-score of a measure X is given by:

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
The mean price for a 2,000sq foot home in FL is $240,000 with a Standard Deviation of $16,000. Home of $200,000.
This means that
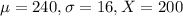 . So
. So

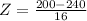

The z-score for a home priced at $200,000 in Florida is of -2.5.
The mean price of the same sized home in OH is $170,000 with a standard deviation of $12,000. Home of $200,000.
This means that
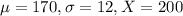 . So
. So

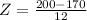

The z-score for a home priced at $200,000 in Ohio is of 2.5.
Which state would a home priced at $200,000 be closer to the mean price, compared to the distribution of prices in the state?
The closeness to the mean is measured by the absolute z-score(disconsidering the signal, the lower the score, the closer to the mean). However, in this case, both z-scores have the same absolute value, so in both Florida and Ohio a home priced at $200,000 is equally close to the mean.