Answer:
The total distance the ball has travelled after it hits the ground the 5th time is of 48.53m.
Explanation:
Geometric sequence:
In a geometric sequence, the quotient of consecutive terms is the same. The nth term of a geometric sequence is given by:
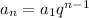
In which
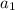 is the first term and
is the first term and
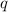 is the common ratio.
is the common ratio.
A super-bouncy-ball is thrown 25m into the air. The ball falls, rebounds to 70% of the height of the previous bounce and falls again.
This means that:
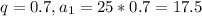
Then
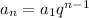
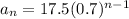
First 5 terms:
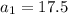
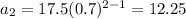
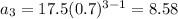

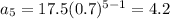
Find the total distance the ball has travelled after it hits the ground the 5th time.
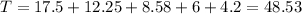
The total distance the ball has travelled after it hits the ground the 5th time is of 48.53m.