Solution :
Demand for cola : 100 – 34x + 5y
Demand for cola : 50 + 3x – 16y
Therefore, total revenue :
x(100 – 34x + 5y) + y(50 + 3x – 16y)
R(x,y) =
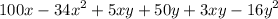
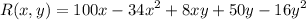
In order to maximize the revenue, set
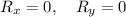
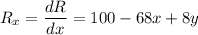
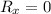
 .............(i)
.............(i)
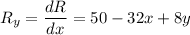
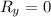
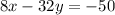 .............(ii)
.............(ii)
Solving (i) and (ii),
4 x (i) ⇒ 272x - 32y = 400
(ii) ⇒ (-) 8x - 32y = -50
264x = 450
∴
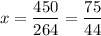
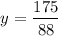
So, x ≈ $ 1.70 and y = $ 1.99
R(1.70, 1.99) = $ 134.94
Thus, 1.70 dollars per cola
1.99 dollars per iced ted to maximize the revenue.
Maximum revenue = $ 134.94