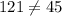Question

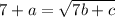1. The equation is of the form , where a, b, and c are all positive integers and . Using this equation as a model, create your own equation that has extraneous solutions. (a) Using trial and error with numbers for a, b, and c, create an equation of the form , where a, b, and c are all positive integers and such that 7 is a solution. (Hint: Substitute 7 for x, and choose a value for a. Then square both sides so you can choose a, b, and c that will make the equation true.) (b) Solve the equation you created in Part 2a. (c) If your solution in Part 2b did not have an extraneous solution, revise your equation so that 7 is one solution and there is an extraneous solution. If your solution in Part 2b did have an extraneous solution, create another equation with different values of a, b, and c that also has 7 as one solution and an extraneous solution.

Answer 1

`7 + a = √(7b + c)` --- equation

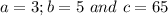`a = 3; b =5\ and\ c = 65` --- the equation is true for these values

`a = 4; b=5\ and\ c = 10` --- the equation is extraneous for these values

Explanation:

Given

`x +2 = \sqrt{3x + 10`

`x + a = √(bx + c)`

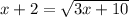
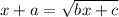
Solving (a): Equation to solve for a, b and c, using trial by error where
`x = 7`

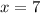
We have:

`x + a = √(bx + c)`

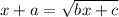
Substitute 7 for x

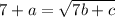`7 + a = √(7b + c)` --- This is the equation

Solving (b): Solve for a, b and c --- to make the equation true

`7 + a = √(7b + c)`

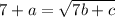
Let a = 3 ----- Here, we choose a value for a

`7 + 3 = √(7b + c)`

`10 = √(7b + c)`

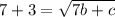
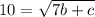
Square both sides

`100 = 7b + c`

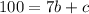
Let b = 5 --------- Here, we choose a value for b

`100 = 7*5 + c`

`100 = 35 + c`

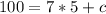
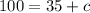
Subtract 35 from both sides

`c = 65`

So,
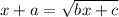`x + a = √(bx + c)` is true for

`a = 3; b =5\ and\ c = 65`

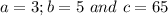
Solving (b): Solve for a, b and c --- to make the equation false

`7 + a = √(7b + c)`

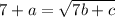
Substitute
`a = 4; b=5\ and\ c = 10`

So, we have:

`7 + 4 = √(7*5 + 10)`

`11 = √(35 + 10)`

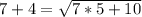
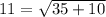
Square both sides

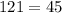`121 = 45` --- This is false

i.e.

`121 \\e 45`