Question

The following function is probability mass function.

x -2 -1 0 1 2
f(x) 1/9 2/9 3/9 2/9 1/9

Required:
Determine the mean and variance of the random variable.

Answer 1

The mean of the random variable is 0.

The variance of the random variable is of 1.11.

Explanation:

We are given the following distribution:

`P(X = -2) = (1)/(9)`

`P(X = -1) = (2)/(9)`

`P(X = 0) = (3)/(9)`

`P(X = 1) = (2)/(9)`

`P(X = 2) = (1)/(9)`

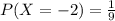
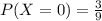
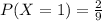
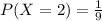
Mean:

Sum of each outcome multiplied by its probability. So

`E(X) = -2(1)/(9) -1(2)/(9) + 0(3)/(9) + 1(2)/(9) + 2(1)/(9) = (-2 - 2 + 0 + 2 + 2)/(9) = 0`

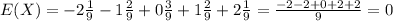
The mean of the random variable is 0.

Variance of the random variable.

Sum of the probability of each outcome multiplied by the difference squared between the outcome and the mean. So

`V(X) = (-2-0)^2(1)/(9) +(-1-0)^2(2)/(9) + (0-0)^2(3)/(9) + (1-0)^2(2)/(9) + (2-0)^2(1)/(9) = (4 + 1 + 0 + 1 + 4)/(9) = 1.11`

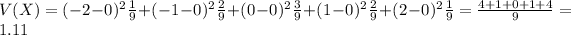
The variance of the random variable is of 1.11.