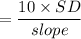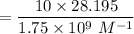Question

Low concentrations of EDTA near the detection limit gave the following dimensionless instrument readings: 175, 104, 164, 193, 131, 189, 155, 133, 151, and 176. Ten blanks had a mean reading of 50.0. The slope of the calibration curve is 1.75 x 10^-9 M^-1.

a. Estimate the signal detection limit for EDTA.
b. What is the concentration detection limit?
c. What is the lower limit of quantification?

Answer 1

Explanation:

From the given information:

The mean of the readings is:
`=(175+104+164+193+131+189+155+133+151+ 176)/(10)`

`= (1571)/(10)`

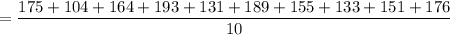
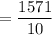
= 157.1

The standard deviation (SD) can be computed by using the expression:

`SD =\sqrt{ (\sum_f(x_i - \bar x)^2)/(n-1)}`

`SD =\sqrt{ ((175-157.1)^2+(104-157.1)^2+(164-157.1)^2+...+(176-157.1)^2)/(10-1)}`

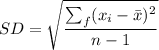
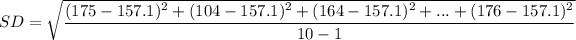
Standard deviation = 28.195

∴

FOr the EDTA complexes;

The signal detection limit = (3*SD) +
`y_(blanks)`

= (3*28.195) + 50

= 84.585 + 50

= 134.585

We need to point out that the value of the calibration curve given is too vague and it should be (1.75 x 10^9 M^-1) as oppose to (1.75 x 10^-9 M^-1)

The concentration of detection limit is:

`=(3 * SD)/(slope )`

`=(3 * 28.195)/(1.75 * 10^(9) \ M^(-1) )`

`\mathbf{= 4.833* 10^(-8) \ M}`

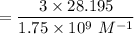
The lower limit of quantification is:

`=(10 * SD)/(slope )`

`=(10 * 28.195)/(1.75 * 10^(9) \ M^(-1) )`

`\mathbf{= 1.611 * 10^(-7) \ M}`