Question

The solution to this system of equations lies between the x-values -2 and -1.5. At which x-value are the two equations approximately equal? y = 1 / x + 2 y = x^2 + 2

Answer 1

Answer: The value of 'x' is -1.8 where the given equation approximately equal

Explanation:

It is given that the value of 'x' lies in the range of -2 to -1.5 and we need to find out the value of 'x' where both the equations become equal

Given set of equations:

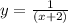`y=(1)/((x+2))` .....(1)

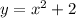`y=x^2+2` .....(2)

Plugging value of 'y' from equation 2 to equation 1:

`x^2+2=(1)/((x+2))\\\\x^2+2(x+2)=1\\\\x^3+2x^2+2x+4=1\\\\x^3+2x^2+2x+3=0`

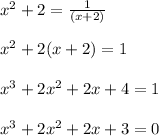
On solving, the real root comes out to be, x = -1.8

Hence, the value of 'x' is -1.8 where the given equation approximately equal