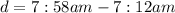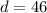Answer:
She walked for 46 minutes
Explanation:
Given
When she leaves home
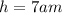
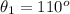
When she arrives at school
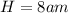
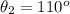
Required
Time to walk to school
First, we convert
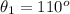 to minutes:
to minutes:


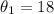 --- approximated
--- approximated
From the question, we understand that she left home past 7.
This means that the difference between the hour hand (at 7) and the minutes hand is 18 minutes.
Also, the minute hand is between 0 and 30 minutes
Subtract 18 minutes from 30 minutes;
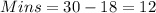
She left home at 7:12am
Similarly;

From the question, we understand that she arrived before 8.
This means that the difference between the hour hand (at 8) and the minutes hand is 18 minutes
Also, the minute hand is between 30 and 60 minutes mark.
At the 8hour hand, the minutes is 40
Add 18 minutes from 40 minutes;
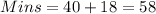
She arrived at 7:58am
The difference (d) is: