Question

Which statement about the graph is true?

O The graph shows a proportional relationship because it is a line, and the difference between each point is the
same

O The graph shows a proportional relationship because it is a line, and each x-value is a multiple of 2.

O The graph does not show a proportional relationship because each point written as a ratio gives a different
value.

O The graph does not show a proportional relationship because a line that increases by 1 in the y-value cannot
have a constant of proportionality.

Answer 1

Explanation:

None of these answers is correct. The graph does not represent a proportional relationship because it does not go through (0, 0).

Answer 2

D. The graph does not show a proportional relationship because a line that increases by 1 in the y-value cannot have a constant of proportionality.

Explanation:

All proportional relationships can be written as
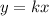`y=kx`, where
`k` is some constant of proportionality. Therefore, all proportional relationships must pass through the origin (0, 0). Since the line shown does not pass through the origin, it cannot be a proportional relationship and we eliminate the first two answer choices.

The graph shows a straight line which represents a linear function, a prerequisite to being a proportional relationship. However, the function for the line is
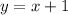`y=x+1`, which is does not follow the format
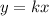`y=kx` and therefore does not pass through the origin. Because of this, the line does not have a constant of proportionality and therefore the answer is D. The graph does not show a proportional relationship because a line that increases by 1 in the y-value cannot have a constant of proportionality.