Question

Your car breaks down in the middle of nowhere. A tow truck weighing 4000 lbs. comes along and agrees to tow your car, which weighs 2000 lbs., to the nearest town. The driver of the truck attaches his cable to your car at an angle of 20 degrees to horizontal. He tells you that his cable has a strength of 500 lbs. He plans to take 10 secs to tow your car at a constant acceleration from rest in a straight line along a flat road until he reaches the maximum speed of 45 m.p.h. Can the driver carry out the plan

Answer 1

F = 1010 Lb

the tension on the cable is greater than its resistance, which is why the plan is not viable

Step-by-step explanation:

For this exercise we can use the kinematic relations to find the acceleration and with Newton's second law find the force to which the cable is subjected.

v = v₀ + a t

how the car comes out of rest v₀ = 0

a = v / t

let's reduce to the english system

v = 45 mph (5280 ft / 1 mile) (1h / 3600) = 66 ft / s

let's calculate

a = 66/10

a = 6.6 ft / s²

now let's write Newton's second law

X axis

Fₓ = ma

with trigonometry

cos 20 = Fₓ / F

Fₓ = F cos 20

we substitute

F cos 20 = m a

F = m a / cos20

W = mg

F =
`(W)/(g) \ (a)/(cos 20)`

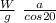
let's calculate

F =
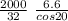`(2000)/(32) \ (6.6 )/(cos20)`(2000/32) 6.6 / cos 20

F = 1010 Lb

Under these conditions, the tension on the cable is greater than its resistance, which is why the plan is not viable.