Question

Find the work done by the gas for the given volume and pressure. Assume that the pressure is inversely proportional to the volume. (See Example 6.) A quantity of gas with an initial volume of 2 cubic feet and a pressure of 1000 pounds per square foot expands to a volume of 3 cubic feet. (Round your answer to two decimal places.)

Answer 1

810.93

Explanation:

Let the pressure be given by P and the volume be V.

Since pressure is inversely proportional to volume, we can write;

P ∝
`(1)/(V)`

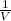
=> P =
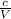`(c)/(V)` -------------(i)

Where;

c = constant of proportionality.

When the volume of the gas is 2 cubic feet, pressure is 1000 pounds per square foot.

V = 2 ft³

P = 1000lb/ft²

Substitute these values into equation (i) as follows;

1000 =
`(c)/(2)`

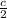
=> c = 2 x 1000

=> c = 2000 lbft

Substituting this value of c back into equation (i) gives

P =
`(2000)/(V)`

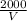
This is the general equation for the relation between the pressure and the volume of the given gas.

To calculate the work done W by the gas, we use the formula

`W = \int\limits^(V_1)_(V_0) {P} \, dV`

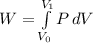
Where;

V₁ = final volume of the gas = 3ft³

V₀ = initial volume of the gas = 2ft³

Substitute P =
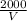`(2000)/(V)`, V₁ = 3ft³ and V₀ = 2ft³

`W = \int\limits^(3)_(2) {(2000)/(V) } \, dV`

Integrate

W = 2000ln[V]³₂

W = 2000(In[3] - ln[2])

W = 2000(0.405465108)

W = 810.93016

W = 810.93 [to 2 decimal places]

Therefore, the work done by the gas for the given pressure and volume is 810.93