Answer:
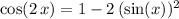 .
.
Explanation:
Angle sum identity for cosine:
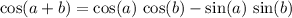 .
.
Pythagorean identity:
 for all real
for all real
 .
.
Subtract
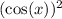 from both sides of the Pythagorean identity to obtain:
from both sides of the Pythagorean identity to obtain:
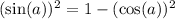 .
.
Apply angle sum identity to rewrite
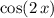 .
.
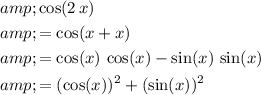 .
.
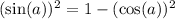 follows from the Pythagorean identity. Hence, it would be possible to replace the
follows from the Pythagorean identity. Hence, it would be possible to replace the
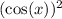 in the previous expression with
in the previous expression with
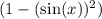 .
.
![\begin{aligned}&(\cos(x))^(2) - (\sin(x))^(2)\\ &= \left[1 - (\sin(x))^(2)\right] - (\sin(x))^(2) \\ &= 1 - 2\, (\sin(x))^(2) \end{aligned}](https://img.qammunity.org/2022/formulas/mathematics/college/hyqmsc0hs1snp5r1g0dcm4j9av9p7n826q.png) .
.
Conclusion:
