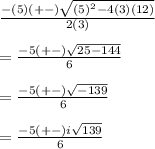Question

Which of the following is a root of the polynomial function below?
F(x) = x+3x2 + 4x+12

Answer 1

`(-5-i√(139))/(6),\ (-5+i√(139))/(6)}`

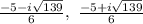
Explanation:

When given the following function,

`F(x)=x+3x^2+4x+12`

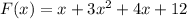
One is asked to find the roots. The roots of the equation are the zeros, where the graph of the equation intersects the (x) axis. To find these points on a quadratic equation (equation to the second degree -> the largest exponent in this equation is (2)), one should simplify the equation. Remember, during simplification, one is trying to get the equation of the parabola closets to the quadratic equation in standard form, this form is the following,

`y=ax^2+bx+c`

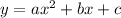
After simplifying the equation, one should use the quadratic formula to find the roots of the equation.

------------------------------------

`F(x)=x+3x^2+4x+12`

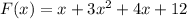
Simplify, combine like terms, terms with the same variable to the same degree;

`F(x)=3x^2+5x+12`

Now use the quadratic formula, the quadratic formula states the following,

`(-b(+-)√(b^2-4ac))/(2a)`

Where the parameters (a), (b, and (c) represent the coefficients of the terms in the quadratic formula in standard form. Substitute in the respective coefficients in the given equation and solve for the roots,

`(-(5)(+-)√((5)^2-4(3)(12)))/(2(3))`

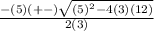
Simplify,

`(-(5)(+-)√((5)^2-4(3)(12)))/(2(3))\\\\=(-5(+-)√(25-144))/(6)\\\\=(-5(+-)√(-139))/(6)\\\\=(-5(+-)i√(139))/(6)`