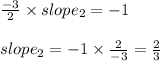Question

What is the slope of a line perpendicular to 3x+2y = 7?​

Answer 1

Slope of the line perpendicular to the given line = 2/3

Explanation:

The product of the slopes of lines perpendicular to each other is - 1

That is,

`slope_(1) * slope _ 2 = - 1\\`

Given equation of the line :

3x + 2y = 7

2y = - 3x + 7

`y = -(3)/(2)x + (7)/(2)`

`Therefore, \ slope \ of \ the \ given \ line \ , slope _1 = \ -(3)/(2)`

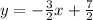
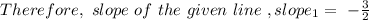
Find slope of the line perpendicular to the given line:

`(-3)/(2) * slope_2 = - 1\\\\slope_2 = - 1 * (2)/(-3) = (2)/(3)`

Answer 2

2/3

Explanation:

First find the slope of the line

3x+2y = 7

Subtract 3x

2y = -3x+7

Divide by 2

y = -3/2x +7/2

This is in slope intercept form y = mx+b where m is the slope

The slope is -3/2

A line perpendicular is the negative reciprocal

-1/(-3/2)

2/3

The slope of the perpendicular line is 2/3