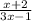Answer:
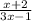
Explanation:
Things you should before solving this question :-
where a and b are any two variables.
SIMPLIFYING THE EXPRESSION
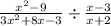
using the identity discussed above
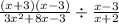
simplifying 3x² + 8x - 3
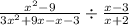
as 8x can be written as 9x - x
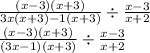
flipping the fraction that follows division sign and inserting multiply in place of divide
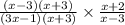
canceling (x - 3) and (x + 3) as they're common in both denominator and numerator