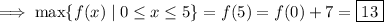Question

The graph of f ′ (x), the derivative of f(x), is continuous for all x and consists of five line segments as shown below. Given f (0) = 6, find the absolute maximum value of f (x) over the interval [0, 5].

2
8
11
13

Answer 1

The maxima of f(x) occur at its critical points, where f '(x) is zero or undefined. We're given f '(x) is continuous, so we only care about the first case. Looking at the plot, we see that f '(x) = 0 when x = -4, x = 0, and x = 5.

Notice that f '(x) ≥ 0 for all x in the interval [0, 5]. This means f(x) is strictly increasing, and so the absolute maximum of f(x) over [0, 5] occurs at x = 5.

By the fundamental theorem of calculus,

`\displaystyle f(5) = f(0) + \int_0^5 f'(x) \, dx`

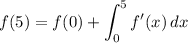
The definite integral corresponds to the area of a trapezoid with height 2 and "bases" of length 5 and 2, so

`\displaystyle \int_0^5 f'(x) \, dx = \frac{5+2}2 * 2 = 7`

`\implies \max\{f(x) \mid 0\le x \le5\} = f(5) = f(0) + 7 = \boxed{13}`