Question

Which linear inequality represents the graph below?

A. x 2² x + 1

B. y2-}x+1

C. >*x+1

D. -*x+1​

Answer 1

Given:

The graph of an inequality.

To find:

The inequality.

Solution:

In the given graph, the boundary line passes through the points (-3,3) and (0,1).

So, the equation of the boundary line is:

`y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)`

`y-3=(1-3)/(0-(-3))(x-(-3))`

`y-3=(-2)/(3)(x+3)`

`y-3=-(2)/(3)(x)-(2)/(3)(3)`

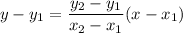
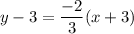
Adding 3 on both sides, we get

`y=-(2)/(3)(x)-2+3`

`y=-(2)/(3)(x)+1`

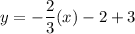
The boundary line is a solid line and the shaded region is above the boundary line. So, the sign of inequality must be
`\geq` and the required inequality is:

`y\geq -(2)/(3)(x)+1`

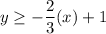
Therefore, the correct option is B.