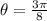Question

Solve each equation for 0 ≤ θ 2π -2√2=-4sin 2θ

Answer 1

Explanation:

Begin by dividing both sides by -4 to get:

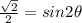`(√(2) )/(2)=sin2\theta` and then take the inverse sin of both sides to get

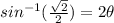`sin^(-1)((√(2) )/(2))=2\theta` (the inverse sin undoes the sin on the right). Now we need to look on our unit circle to find the angles where
`sin((√(2) )/(2))` is positive. There are 2 places. Sin is positive in both QI and QII. The angles are

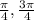`(\pi)/(4),(3\pi)/(4)`. Therefore, our 2 equations are

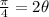`(\pi)/(4)=2\theta` and
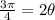`(3\pi)/(4)=2\theta`. Solving the first equation:

`\theta=(\pi)/(8)`

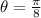
and the second equation:

`\theta=(3\pi)/(8)`