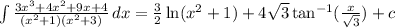Answer:
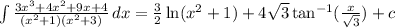
Explanation:
Given
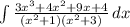
Required
Integrate
Using partial fraction, we have:
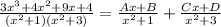
Take LCM
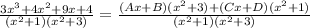
Cancel out the denominators
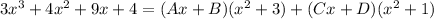
Open brackets
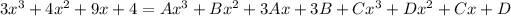
Collect like terms
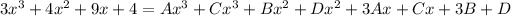
Compare like terms on opposite sides
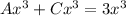
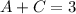
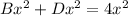
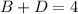
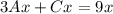
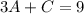
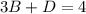
Subtract
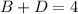 from
from
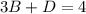
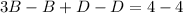
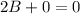
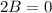
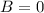
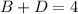
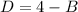
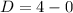
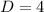
Subtract
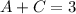 from
from
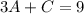
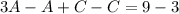
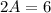
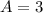
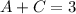
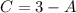
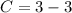
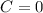
So, we have:
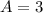
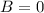
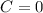
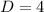
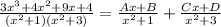
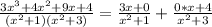
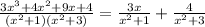
The integral becomes:
![\int\limits {[(3x)/(x^2 + 1) + (4)/(x^2 + 3)]} \, dx](https://img.qammunity.org/2022/formulas/mathematics/college/79j18mhhd9kao9qpk27bjuzhmwwxakgzr8.png)
Split:
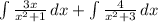
Split
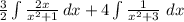
Integrate
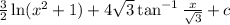
Hence: