Question

Solve the following trigonometric equation over the interval of [0,2π). Show your work, thank you!


`\large{2sin \theta tan \theta = - 3}`
​

Answer 1

`\rm \displaystyle \theta = \{ {150}^( \circ) , {240}^( \circ) \}`

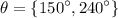
Explanation:

we would like to solve the following equation:

`\displaystyle 2 \sin( \theta) \tan( \theta) = - 3`

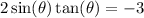
to do so we need to put the equation in term of a function of a angle therefore rewrite tanθ:

`\displaystyle 2 \sin( \theta) \cdot ( \sin( \theta) )/( \cos( \theta) ) = - 3`

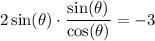
simplify multiplication:

`\displaystyle ( 2\sin^(2) ( \theta) )/( \cos( \theta) ) = - 3`

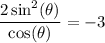
cross multiplication:

`\displaystyle 2\sin^(2) ( \theta) = - 3 \cos( \theta)`

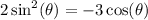
isolate -3cosθ to left hand side and change its sign:

`\displaystyle 2\sin^(2) ( \theta) + 3 \cos( \theta) = 0`

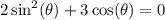
well we can rewrite sin²θ by applying Pythagorean theorem and that yields:

`\rm \displaystyle 2(1 - \cos^(2) ( \theta)) + 3 \cos( \theta) = 0`

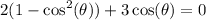
distribute:

`\rm \displaystyle 2 - 2\cos^(2) ( \theta) + 3 \cos( \theta) = 0`

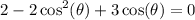
now notice that our equation ended up with a pattern and that is Quadratic thus by letting cosθ be x to transform the equation:

`\rm \displaystyle 2 - 2 {x}^(2) + 3 x = 0`

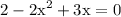
rearrange it to standard form:

`\rm \displaystyle - 2 {x}^(2) + 3 x + 2 = 0`

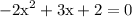
divide both sides by -1:

`\rm \displaystyle 2 {x}^(2) - 3 x - 2 = 0`

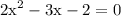
well we can factor the quadratic to do so rewrite -3x as -4x+x:

`\rm \displaystyle 2 {x}^(2) - 4 x + x - 2 = 0`

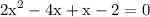
factor out 2x:

`\rm \displaystyle 2x ({x}^{} - 2)+ x - 2 = 0`

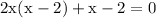
factor out 1:

`\rm \displaystyle 2x ({x}^{} - 2)+ 1(x - 2 ) = 0`

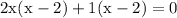
group:

`\rm \displaystyle (2x + 1)(x - 2 ) = 0`

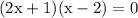
by Zero Product property we obtain:

`\rm \displaystyle \begin{cases} 2x + 1 = 0\\ x - 2 = 0 \end{cases}`

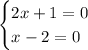
cancel 1 from the first equation and add 2 to the e equation:

`\rm \displaystyle \begin{cases} 2x = - 1\\ x = 2\end{cases}`

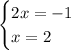
substitute back:

`\rm \displaystyle \begin{cases} 2 \cos( \theta) = - 1\\ \cos( \theta) = 2\end{cases}`

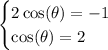
since cosθ is only defined for the interval [1,-1] the second equation is false for any value of θ but we can still continue the first equation

`\rm \displaystyle \begin{cases} 2 \cos( \theta) = - 1\\ \cos( \theta) \\eq 2\end{cases}`

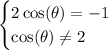
divide both sides by 2:

`\rm \displaystyle \cos( \theta) = \frac{ - 1} {2}`

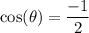
by unit circle we acquire:

`\begin{cases} \rm \displaystyle \theta = {150}^( \circ) \\ \theta = {240}^( \circ) \end{cases}`

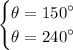
add period of 2nπ:

`\begin{cases} \rm \displaystyle \theta = {150}^( \circ) + 2n\pi\\ \theta = {240}^( \circ) + 2n\pi \end{cases}`

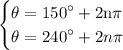
for the interval [0,2π) θ is only defined when n is 0 Thus:

`\begin{cases} \rm \displaystyle \theta = {150}^( \circ) + 2(0)\pi\\ \theta = {240}^( \circ) + 2(0)\pi \end{cases}`

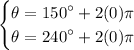
simplify:

`\begin{cases} \rm \displaystyle \theta = {150}^( \circ) \\ \theta = {240}^( \circ) \end{cases}`

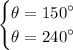
hence,

θ is equal to 150° and 240°