Answer:
Explanation:
5). 3x + y = 5 -------(1)
2x - y = 10 ---------(2)
By adding equation (1) and (2),
(3x + y) + (2x - y) = 5 + 10
5x = 15
x = 3
From equation (1),
3(3) + y = 5
y = -4
6). 4x + 3y = 13 -------(1)
x + y = 4 -------(2)
Multiply equation (2) by 3 and subtract it from equation (1)
(4x + 3y) - (3x + 3y) = 13 - 12
x = 1
From equation (2),
1 + y = 4
y = -3
7). x - 7y = 7 -----(1)
-3x + 21y = -21
-3(x - 7y) = -(3 × 7)
x - 7y = 7 -------(2)
Since, equation (1) and (2) are same, system of the equations will have infinitely many solutions.
8). x - 3y = 12
3y = x - 12
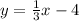 --------(1)
--------(1)
3x - 9y = 18
3(x - 3y) = 3(6)
x - 3y = 6
3y = x - 6
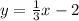 ----------(2)
----------(2)
Slopes of both the equations are same but the y-intercepts are different.
Therefore, both the lines are parallel and the system of equations will have no solution.