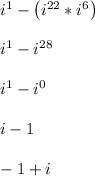Question

Please help with imaginary numbers worksheet!

Answer 1

Answer -1 for number 7

Answer 2

Problem 5

Answer: 6i

------------------

Step-by-step explanation:

We have these four identities

• i^0 = 1
• i^1 = i
• i^2 = -1
• i^3 = -i

Notice how computing i^4 leads us back to 1. So i^4 = i^0. The pattern repeats every 4 terms. So we divide the exponent by 4 and look at the remainder. We ignore the quotient entirely. We can see that 28/4 = 7 remainder 0. Meaning that i^28 = i^0 = 1.

We can think of it like this if you wanted

i^28 = (i^4)^7 = 1^7 = 1

Then the sqrt(-36) becomes 6i

So overall, we end up with the final answer of 6i

=============================================

Problem 6

Answer: -3i

------------------

Step-by-step explanation:

We'll use the ideas mentioned in problem 5

46/4 = 11 remainder 2

i^46 = i^2 = -1

sqrt(-9) = 3i

The two outside negative signs cancel out, but there's still a negative from -1 we found earlier. So we end up with -3i

In other words, here is one way you could write out the steps

`-i^(46)*-√(-9)\\\\-i^(2)*-3i\\\\i^(2)*3i\\\\-1*3i\\\\-3i\\\\`

=============================================

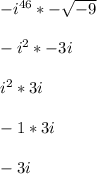
Problem 7

Answer: -1

------------------

Work Shown:

i^10 = i^2 because 10/4 = 2 remainder 2

i^19 = i^3 because 19/4 = 4 remainder 3

i^7 = i^3 because 7/4 = 1 remainder 3

Again, all we care about are the remainders.

`i^(10)+i^(19) - i^(7)\\\\i^(2)+i^(3) - i^(3)\\\\i^(2)\\\\-1`

=============================================

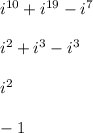
Problem 8

Answer: -1 + i

------------------

Work Shown:

i^22*i^6 = i^(22+6) = i^28

Earlier in problem 5, we found that i^28 = i^0 = 1

So,

`i^1 - \left(i^(22)*i^(6)\right)\\\\i^1 - i^(28)\\\\i^1 - i^(0)\\\\i - 1\\\\-1+i`