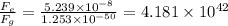Question

Two electrons in adjacent atomic shells are separated by a distance of 6.64 ✕ 10−11 m. (a) What is the magnitude of the electrostatic force between the electrons? N (b) What is the ratio of the electrostatic force to the gravitational force between the electrons? FE FG =

Answer 1

The ratio of the electrostatic force to the gravitational force between the electrons is 4.181 x 10⁴²

Step-by-step explanation:

Given;

charge of electron, Q = 1.602 x 10⁻¹⁹ C

mass of an electron, m = 9.1 x 10⁻³¹ kg

distance between the two electrons, r = 6.64 x 10⁻¹¹ m

The electrostatic force between the electrons is calculated using Coulomb's law;

`F_e = (kQ^2)/(r^2) \\\\F_e = ((9* 10^9)(1.602 * 10^(-19))^2)/((6.64 * 10^(-11))^2) \\\\F_e = 5.239 * 10^(-8) \ N`

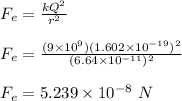
The gravitaional force between the electrons is calculated as;

`F_g = (Gm^2)/(r^2) \\\\F_g = ((6.67* 10^(-11))(9.1 * 10^(-31))^2)/((6.64* 10^(-11))^2) \\\\F_g = 1.253 * 10^(-50) \ N`

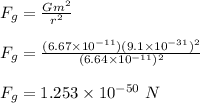
The ratio of the electrostatic force to the gravitational force between the electrons;

`(F_e)/(F_g) = (5.239* 10^(-8))/(1.253 * 10^(-50)) = 4.181 * 10^(42)`