Answer:
Length: 12 meters
Explanation:
Step 1:
Let us start with the formula of the perimeter of a rectangle,
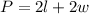 , where l represents the length of the rectangle, and w represents the width of the rectangle.
, where l represents the length of the rectangle, and w represents the width of the rectangle.
We can set width as variable x. We are also given that the length is three times the width, hence it can be represented as 3x.
Step 2:
We can now write our equation and solve for x :
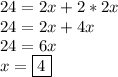
We set x as width, so the width is 4 meters. However, in this problem we are looking for the length. The length is three times the width, so it would be
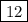 meters.
meters.
I hope this helps! Let me know if you have any questions :)