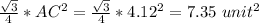Question

Triangle ABC is an equilateral triangle with vertices at A(-2,2), B(1,5), and C(-3,6) (Round your answers to the nearest hundredth, 2 decimal places) . a) (2 pts) Determine the length of a side of the triangle. b) (2 pts) Calculate the perimeter of the triangle. c) (2 pts) Now increase the triangle by a scale factor of 4. How long is each side now? d) (2 pts) What is the perimeter of the new triangle? e) (2 pts) What is the area of the original triangle?

Answer 1

The answer is below

Explanation:

The distance between two points A(x₁, y₁) and B(x₂, y₂) on the coordinate is:

`Distance=√((x_2-x_1)^2+(y_2-y_1)^2) \\\\`

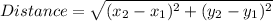
An equilateral triangle is a triangle with three equal sides (all sides are equal).

a) Given vertices at A(-2,2), B(1,5), and C(-3,6):

`AC=√((-3-(-2))^2+(6-2)^2)=√(1+16)=√(17)=4.12\ unit\\\\AB=BC=AC=4.12\ unit`

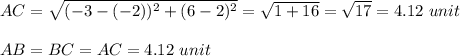
b) Perimeter = AB + BC + AC = 3 * AC = 3 * 4.12 = 12.36 unit

c) If the scale factor is increased by 4, all the sides would also increase by 4. Hence the new length would be:

A'B' = B'C' = A'C' = 4 * AC = 4 * 4.12 = 16.48 unit

d) Perimeter = A'B' + B'C' + A'C' = 3 * A'C' = 3 * 16.48 = 49.44 unit

e) Area =
`(√(3) )/(4)*AC^2=(√(3) )/(4) *4.12^2=7.35\ unit^2`