Question

Solve the system of equations by graphing on a separate sheet of paper. Write your solutions as ordered pairs from least to greatest with respect to the x-coordinate.

y=x2−4x+1
y=x−3

Answer 1

(1, -2), (4, 1)

Explanation:

Here we want to solve the system of equations:

y = x^2 - 4*x + 1

y = x - 3

First, we can see that in both parts we have isolated the variable "y", so we can just write:

x - 3 = y = x^2 - 4*x + 1 = y

removing the "y"s, we get:

x - 3 = x^2 - 4*x + 1

Now we can solve this for x

0 = x^2 - 4*x + 1 - x + 3

0 = x^2 - 5*x + 4

This is a quadratic equation, the solutions are given by the Bhaskara's formula, that says that for a general quadratic equation:

0 = a*x^2 + b*x + c

The solutions are given by:

`x = (-b \pm √(b^2 - 4*a*c) )/(2*a)`

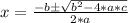
So for the case of our equation:

0 =x^2 - 5*x + 4

The solutions are given by:

`x = (-(-5) \pm √((-5)^2 - 4*1*4) )/(2*1) = (5 \pm 3)/(2)`

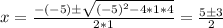
So the two solutions are:

x₁ = (5 + 3)/2 = 4

x₂ = (5 - 3)/2 = 1

To find the ordered pair, we need to replace these values in one of the equations of the system, let's use the second:

y = x₁ - 3 = 4 - 3 = 1

Then we have one solution at (4, 1)

And for the other:

y = x₂ - 3 = 1 - 3 = -2

then the ordered pair is (1, -2)

Now we want to write from least to greatest with respect to the x-coordinate, then the correct order is:

(1, -2), (4, 1)