Given:
Ratio of the side lengths of two similar rectangular prisms is
 .
.
To find:
The ratio of their areas.
Solution:
If two figures are similar then their areas are proportional to the squares of their corresponding sides.
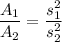
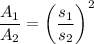 ...(i)
...(i)
Where,
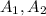 are areas and
are areas and
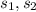 are corresponding sides.
are corresponding sides.
It is given that ratio of the side lengths of two similar rectangular prisms is
 . It means,
. It means,
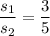 .
.
Using (i), we get
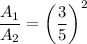

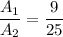
Therefore, the ratio of their areas is
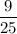 . It is also written as 9:25.
. It is also written as 9:25.